Understanding and calculating variance

Published on September 24, 2020 by Pritha Bhandari. Revised on October 12, 2020.

The variance is a measure of variability. It is calculated by taking the average of squared deviations from the mean.

Variance tells you the degree of spread in your data set. The more spread the data, the larger the variance is in relation to the mean.

Variance vs standard deviation

The standard deviation is derived from variance and tells you, on average, how far each value lies from the mean. It's the square root of variance.

Both measures reflect variability in a distribution, but their units differ:

  • Standard deviation is expressed in the same units as the original values (e.g., meters).
  • Variance is expressed in much larger units (e.g., meters squared)

Since the units of variance are much larger than those of a typical value of a data set, it's harder to interpret the variance number intuitively. That's why standard deviation is often preferred as a main measure of variability.

However, the variance is more informative about variability than the standard deviation, and it's used in making statistical inferences.

Population vs sample variance

Different formulas are used for calculating variance depending on whether you have data from a whole population or a sample.

Population variance

When you have collected data from every member of the population that you're interested in, you can get an exact value for population variance.

The population variance formula looks like this:

Formula Explanation
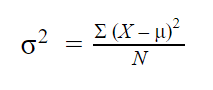Variance formula for populations
  • σ2 = population variance
  • Σ = sum of…
  • Χ= each value
  • μ = population mean
  • Ν = number of values in the population

Sample variance

When you collect data from a sample, the sample variance is used to make estimates or inferences about the population variance.

The sample variance formula looks like this:

Formula Explanation
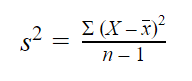Variance formula for samples
  • s2 = sample variance
  • Σ = sum of…
  • Χ= each value
  • x̄ = sample mean
  • n = number of values in the sample

With samples, we use n – 1 in the formula because using n would give us a biased estimate that consistently underestimates variability. The sample variance would tend to be lower than the real variance of the population.

Reducing the sample n to n – 1 makes the variance artificially large, giving you an unbiased estimate of variability: it is better to overestimate rather than underestimate variability in samples.

It's important to note that doing the same thing with the standard deviation formulas doesn't lead to completely unbiased estimates. Since a square root isn't a linear operation, like addition or subtraction, the unbiasedness of the sample variance formula doesn't carry over the sample standard deviation formula.

Receive feedback on language, structure and formatting

Professional editors proofread and edit your paper by focusing on:

  • Academic style
  • Vague sentences
  • Grammar
  • Style consistency

See an example

Steps for calculating the variance

The variance is usually calculated automatically by whichever software you use for your statistical analysis. But you can also calculate it by hand to better understand how the formula works.

There are five main steps for finding the variance by hand. We'll use a small data set of 6 scores to walk through the steps.

Data set
46 69 32 60 52 41

Step 1: Find the mean

To find the mean, add up all the scores, then divide them by the number of scores.

Mean (x̅)
x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50

Step 2: Find each score's deviation from the mean

Subtract the mean from each score to get the deviations from the mean.

Since x̅ = 50, take away 50 from each score.

Score Deviation from the mean
46 46 – 50 = -4
69 69 – 50 = 19
32 32 – 50 = -18
60 60 – 50 = 10
52 52 – 50 = 2
41 41 – 50 = -9

Step 3: Square each deviation from the mean

Multiply each deviation from the mean by itself. This will result in positive numbers.

Squared deviations from the mean
(-4)2 = 4 × 4 = 16
192 = 19 × 19 = 361
(-18)2 = -18 × -18 = 324
102 = 10 × 10 = 100
22 = 2 × 2 = 4
(-9)2 = -9 × -9 = 81

Step 4: Find the sum of squares

Add up all of the squared deviations. This is called the sum of squares.

Sum of squares
16 + 361 + 324 + 100 + 4 + 81 = 886

Step 5: Divide the sum of squares byn – 1 or N

Divide the sum of the squares by n – 1 (for a sample) or N (for a population).

Since we're working with a sample, we'll use n – 1, where n = 6.

Variance
 886 ÷ (6 – 1) = 886 ÷ 5 = 177.2

Why does variance matter?

Variance matters for two main reasons:

  • Parametric statistical tests are sensitive to variance.
  • Comparing the variance of samples helps you assess group differences.

Homogeneity of variance in statistical tests

Variance is important to consider before performing parametric tests. These tests require equal or similar variances, also called homogeneity of variance or homoscedasticity, when comparing different samples.

Uneven variances between samples result in biased and skewed test results. If you have uneven variances across samples, non-parametric tests are more appropriate.

Using variance to assess group differences

Statistical tests like variance tests or the analysis of variance (ANOVA) use sample variance to assess group differences. They use the variances of the samples to assess whether the populations they come from differ from each other.

Research example
As an education researcher, you want to test the hypothesis that different frequencies of quizzes lead to different final scores of college students. You collect the final scores from three groups with 20 students each that had quizzes frequently, infrequently, or rarely over a semester.
  • Sample A: Once a week
  • Sample B: Once every 3 weeks
  • Sample C: Once every 6 weeks

To assess group differences, you perform an ANOVA.

The main idea behind an ANOVA is to compare the variances between groups and variances within groups to see whether the results are best explained by the group differences or by individual differences.

If there's higher between-group variance relative to within-group variance, then the groups are likely to be different as a result of your treatment. If not, then the results may come from individual differences of sample members instead.

Research example
Your ANOVA assesses whether the differences in mean final scores between groups come from the differences in the frequency of quizzes or the individual differences of the students in each group.

To do so, you get a ratio of the between-group variance of final scores and the within-group variance of final scores – this is the F-statistic. With a large F-statistic, you find the corresponding p-value, and conclude that the groups are significantly different from each other.

Frequently asked questions about variance

What is homoscedasticity?

Homoscedasticity, or homogeneity of variances, is an assumption of equal or similar variances in different groups being compared.

This is an important assumption of parametric statistical tests because they are sensitive to any dissimilarities. Uneven variances in samples result in biased and skewed test results.

Is this article helpful?

You have already voted. Thanks :-) Your vote is saved :-) Processing your vote...